
Example 6 Classify A Conic Ppt Video Online Download
Answer (1 of 4) The graph of x^2(y\sqrt3{x^2})^2=1 is very interesting and is shown below using desmosVIDEO ANSWER Sketch a graph of 4(y2)=xx1 Get 24/7 study help with the Numerade app for iOS and Android!
X^2+y^2=4y graph
X^2+y^2=4y graph-Solution for Find the domain for the function fix,y) 1) f(x, y)In (5x4y) Match the surface show below to the graph of its level curves 2)X = −y2 4y x = y 2 4 y Find the properties of the given parabola Tap for more steps Direction Opens Left Vertex (4,2) ( 4, 2) Focus (15 4,2) ( 15 4, 2) Axis of Symmetry y = 2 y =

How Do You Graph X 2 Y 2 4 Socratic
X^2 y^2 8x 4y = 29 completing the square (x^28x16) (y^24y4)= (x4)^2 (y2)^2=49 This is a Steps to graph x^2 y^2 = 4The first graph is symmetric at the point x and in the second graph is since it isn't invertible the inverse is not a function because it fails the VLT d) The graphs above are symmetric at the line
X^{2}3y^{2}x1=0 \frac{(x2)^{2}}{}\frac{y^{2}}{36}=1 DetailedFree PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep Graph the circle x^2y^24y60=0 tjordan6499 is waiting for your help Add your answer and earn points
X^2+y^2=4y graphのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
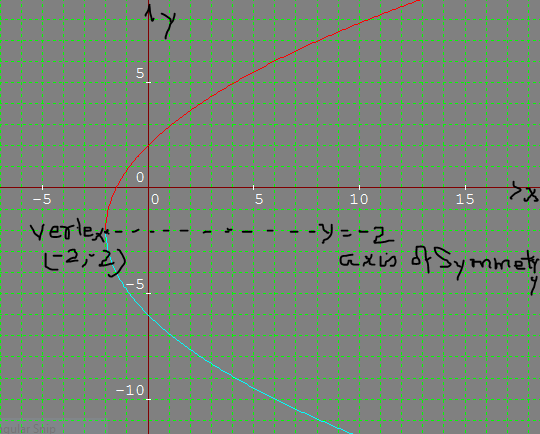 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
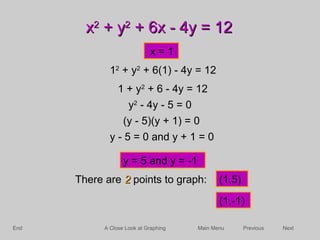 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
「X^2+y^2=4y graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | 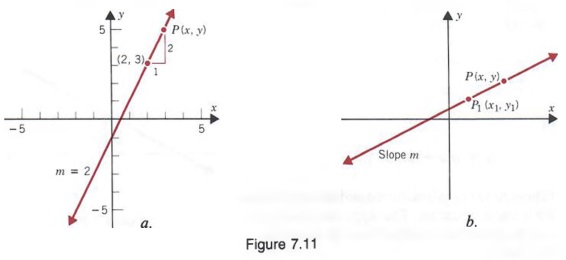 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | 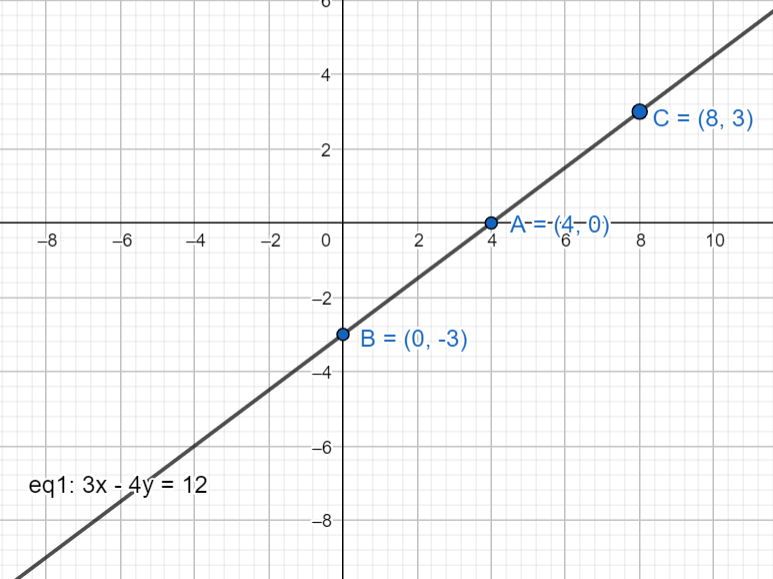 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
「X^2+y^2=4y graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
「X^2+y^2=4y graph」の画像ギャラリー、詳細は各画像をクリックしてください。
How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | 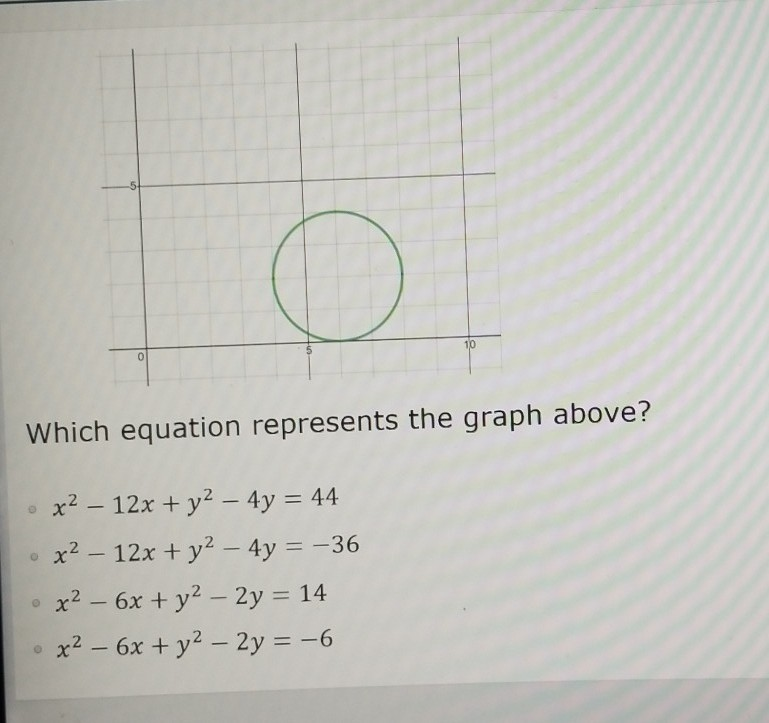 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
「X^2+y^2=4y graph」の画像ギャラリー、詳細は各画像をクリックしてください。
How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
「X^2+y^2=4y graph」の画像ギャラリー、詳細は各画像をクリックしてください。
How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | 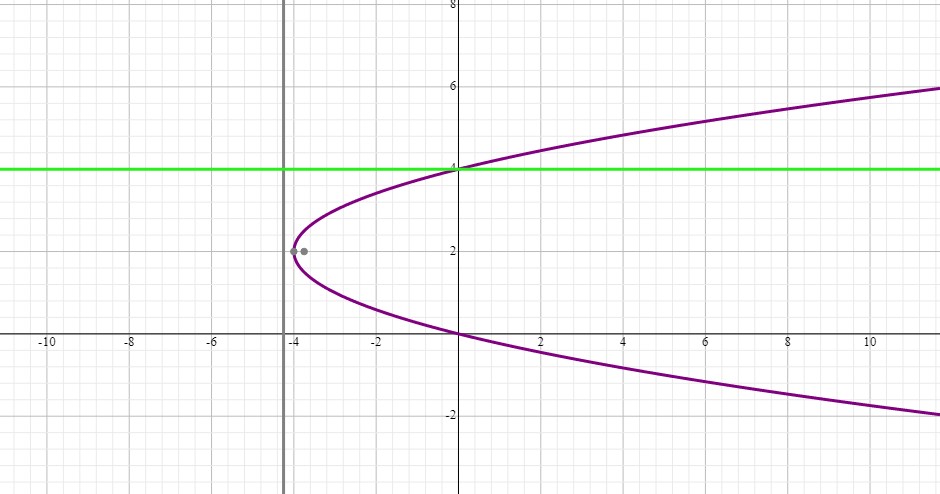 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
「X^2+y^2=4y graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
「X^2+y^2=4y graph」の画像ギャラリー、詳細は各画像をクリックしてください。
How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
「X^2+y^2=4y graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
「X^2+y^2=4y graph」の画像ギャラリー、詳細は各画像をクリックしてください。
How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | 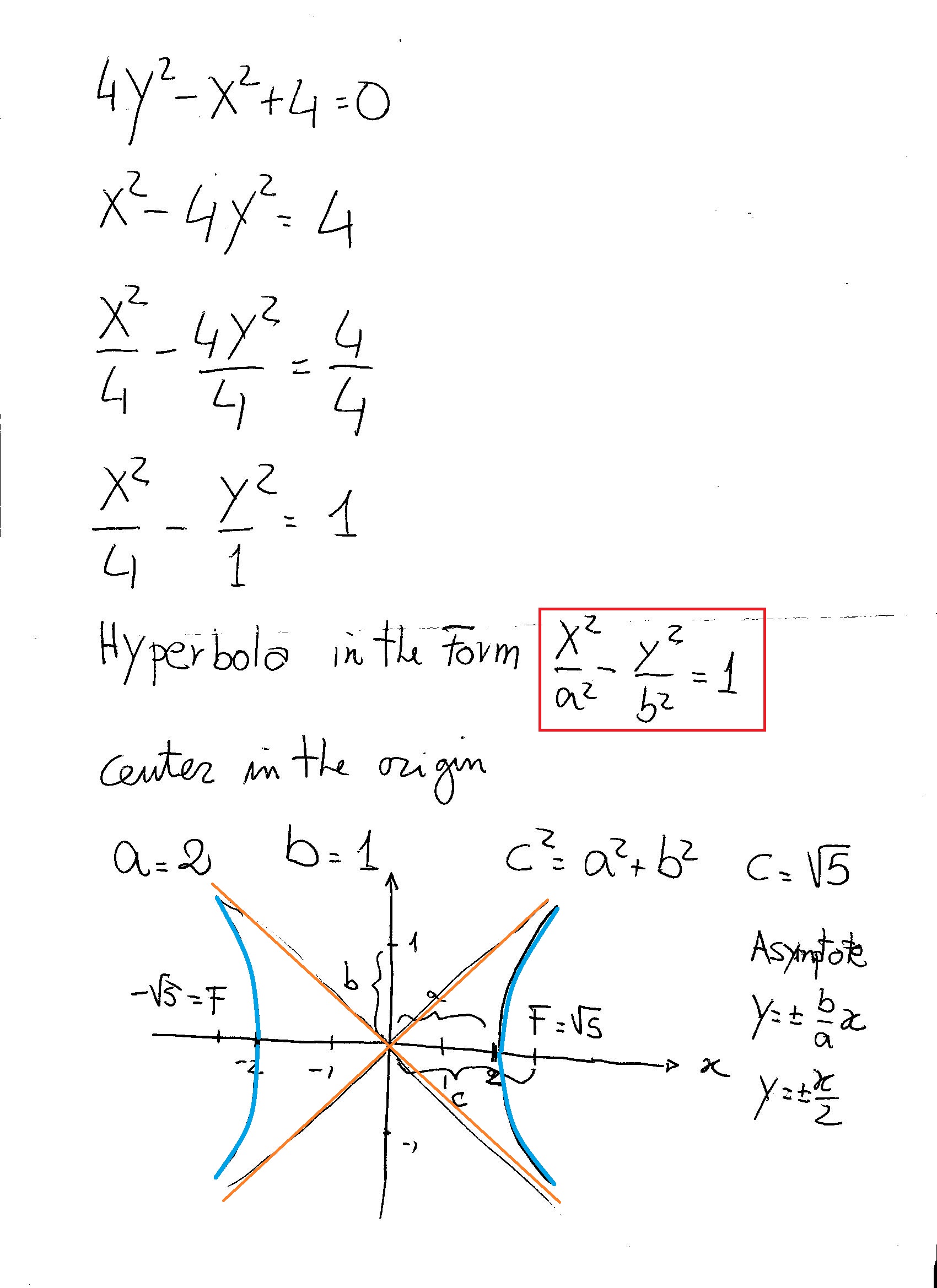 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
「X^2+y^2=4y graph」の画像ギャラリー、詳細は各画像をクリックしてください。
How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic | How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
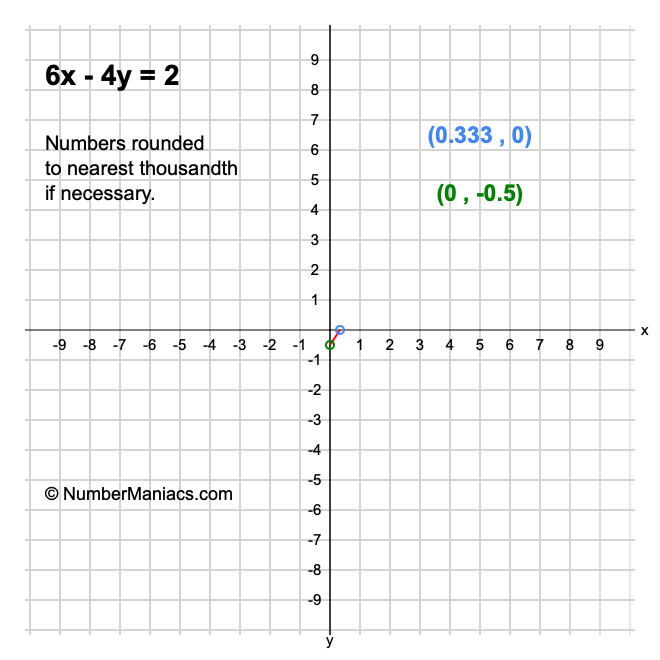 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
「X^2+y^2=4y graph」の画像ギャラリー、詳細は各画像をクリックしてください。
How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
 How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |  How Do You Solve 3x 2y 8 6x 4y 16 By Graphing And Classify The System Socratic |
This is the equation of a circle, center C = (1,2) and radius r = 3 The graph is shown below graph { (x^2y^22x4y4)=0 8065, 7735, 218, 572} Answer linkEnter your email for an invite
Incoming Term: x^2+y^2=4y graph, x^2+4y^2 graph, how to graph x^2+y^2+4y=0, graph the circle x^2+y^2+6x-4y+9=0, graph the circle x^2+y^2+2x-4y-11=0, graph the circle x^2+y^2+2x-4y-4=0,




0 件のコメント:
コメントを投稿